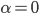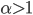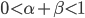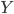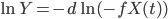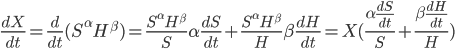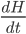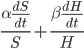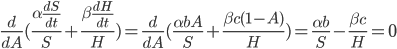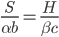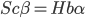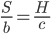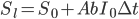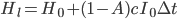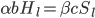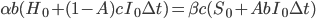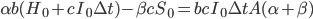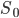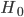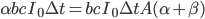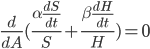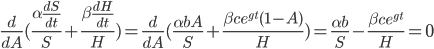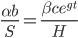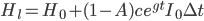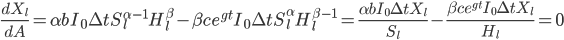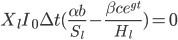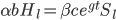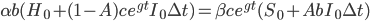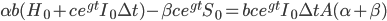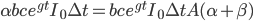The possibility of recursive self-improvement is often brought up as a reason to expect that an intelligence explosion is likely to result in a singleton - a single dominant agent controlling everything. Once a sufficiently general artificial intelligence can make improvements to itself, it begins to acquire a compounding advantage over rivals, because as it increases its own intelligence, it increases its ability to increase its own intelligence. If returns to intelligence are not substantially diminishing, this process could be quite rapid. It could also be difficult to detect in its early stages because it might not require a lot of exogenous inputs.
However, this argument only holds if self-improvement is not only a rapid route to AI progress, but the fastest route. If an AI participating in the broader economy could make advantageous trades to improve itself faster than a recursively self-improving AI could manage, then AI progress would be coupled to progress in the broader economy.
If algorithmic progress (and anything else that might seem more naturally a trade secret than a commodity component) is shared or openly licensed for a fee, then a cutting-edge AI can immediately be assembled whenever profitable, making a single winner unlikely. However, if leading projects keep their algorithmic progress secret, then the foremost project could at some time have a substantial intelligence advantage over its nearest rival. If an AI project attempting to maximize intelligence growth would devote most of its efforts towards such private improvements, then the underlying dynamic begins to resemble the recursive self-improvement scenario.
This post reviews a prior mathematization of the recursive self-improvement model of AI takeoff, and then generalizes it to the case where AIs can allocate their effort between direct self-improvement and trade.
A recalcitrance model of AI takeoff
In Superintelligence, Nick Bostrom describes a simple model of how fast an intelligent system can become more intelligent over time by working on itself. This exposition loosely follows the one in the book.
We can model the intelligence of the system as a scalar quantity  , and the work, or optimization power, applied to system in order to make it more intelligent, as another quantity
, and the work, or optimization power, applied to system in order to make it more intelligent, as another quantity  . Finally, at any given point in the process, it takes some amount of work to augment the system's intelligence by one unit. Call the marginal cost of intelligence in terms of work recalcitrance,
. Finally, at any given point in the process, it takes some amount of work to augment the system's intelligence by one unit. Call the marginal cost of intelligence in terms of work recalcitrance,  , which may take different values at different points in the progress. So, at the beginning of the process, the rate at which the system's intelligence increases is determined by the equation
, which may take different values at different points in the progress. So, at the beginning of the process, the rate at which the system's intelligence increases is determined by the equation  .
.
We then add two refinements to this model. First, assume that intelligence is nothing but a type of optimization power, so  and
and  can be expressed in the same units. Second, if the intelligence of the system keeps increasing without limit, eventually the amount of work it will be able to put into things will far exceed that of the team working on it, so that
can be expressed in the same units. Second, if the intelligence of the system keeps increasing without limit, eventually the amount of work it will be able to put into things will far exceed that of the team working on it, so that  .
.  is now the marginal cost of intelligence in terms of applied intelligence, so we can write
is now the marginal cost of intelligence in terms of applied intelligence, so we can write  .
.
Constant recalcitrance
The simplest model assumes that recalcitrance is constant,  . Then
. Then  , or
, or  . This implies exponential growth.
. This implies exponential growth.
Declining recalcitrance
Superintelligence also considers a case where work put into the system yields increasing returns. Prior to takeoff, where  , this would look like a fixed team of researchers with a constant budget working on a system that always takes the same interval of time to double in capacity. In this case we can model recalcitrance as
, this would look like a fixed team of researchers with a constant budget working on a system that always takes the same interval of time to double in capacity. In this case we can model recalcitrance as  , so that
, so that  , so that
, so that  for some constant
for some constant  , which implies that the rate of progress approaches infinity as
, which implies that the rate of progress approaches infinity as  approaches
approaches  ; a singularity.
; a singularity.
How plausible is this scenario? In a footnote, Bostrom brings up Moore's Law as an example of increasing returns to input, although (as he mentions) in practice it seems like increasing resources are being put into microchip development and manufacturing technology, so the case for increasing returns is far from clear-cut. Moore's law is predicted by the experience curve effect, or Wright's Law, where marginal costs decline as cumulative production increases; the experience curve effect produces exponentially declining costs under conditions of exponentially accelerating production. This suggests that in fact accelerating progress is due to an increased amount of effort put into making improvements. Nagy et al. 2013 show that for a variety of industries with exponentially declining costs, it takes less time for production to double than for costs to halve.
Since declining costs also reflect broader technological progress outside the computing hardware industry, the case for declining recalcitrance as a function of input is ambiguous.
Increasing recalcitrance
In many cases where work is done to optimize a system, returns diminish as cumulative effort increases. We might imagine that high intelligence requires high complexity, and more intelligent systems require more intelligence to understand well enough to improve at all. If we model diminishing returns to intelligence as  , then
, then  . In other words, progress is a linear function of time and there is no acceleration at all.
. In other words, progress is a linear function of time and there is no acceleration at all.
Generalized expression
The recalcitrance model can be restated as a more generalized self-improvement process with the functional form  :
:
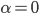 |
Increasing recalcitrance |
Constant progress |
 |
Increasing recalcitrance |
Polynomial progress |
 |
Constant recalcitrance |
Exponential progress |
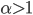 |
Declining recalcitrance |
Singularity |
Deciding between trade and self-improvement
Some inputs to an AI might be more efficiently obtained if the AI project participates in the broader economy, for the same reason that humans often trade instead of making everything for themselves. This section lays out a simple two-factor model of takeoff dynamics, where an AI project chooses how much to engage in trade.
Suppose that there are only two inputs into each AI: computational hardware available for purchase, and algorithmic software that the AI can best design for itself. Each AI project is working on a single AI running on a single hardware base. The intelligence of this AI depends both on hardware progress and software progress, and holding either constant, the other has diminishing returns. (This is broadly consistent with trends described by Grace 2013.) We can model this as  .
.
At each moment in time, the AI can choose whether to allocate all its optimization power to making money in order to buy hardware, improving its own algorithms, or some linear combination of these. Let the share of optimization power devoted to algorithmic improvement be  .
.
Assume further that hardware earned and improvements to software are both linear functions of the optimization power invested, so  , and
, and  .
.
What is the intelligence-maximizing allocation of resources  ?
?
This problem can be generalized to finding  that maximizes
that maximizes  for any monotonic function
for any monotonic function  . This is maximized whenever
. This is maximized whenever  is maximized. (Note that this is no longer limited to the case of diminishing returns.)
is maximized. (Note that this is no longer limited to the case of diminishing returns.)
This generalization is identical to the Cobb-Douglas production function in economics. If  then this model predicts exponential growth, if
then this model predicts exponential growth, if  it predicts a singularity, and if
it predicts a singularity, and if 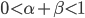 then it predicts polynomial growth. The intelligence-maximizing value of
then it predicts polynomial growth. The intelligence-maximizing value of  is
is  .
.
In our initial toy model  , where
, where  , that implies that no matter what the price of hardware, as long as it remains fixed and the indifference curves are shaped the same, the AI will always spend exactly half its optimizing power working for money to buy hardware, and half improving its own algorithms.
, that implies that no matter what the price of hardware, as long as it remains fixed and the indifference curves are shaped the same, the AI will always spend exactly half its optimizing power working for money to buy hardware, and half improving its own algorithms.
Changing economic conditions
The above model makes two simplifying assumptions: that the application of a given amount of intelligence always yields the same amount in wages, and that the price of hardware stays constant. This section relaxes these assumptions.
Increasing productivity of intelligence
We might expect the productivity of a given AI to increase as the economy expands (e.g. if it discovers a new drug, that drug is more valuable in a world with more or richer people to pay for it). We can add a term exponentially increasing over time to the amount of hardware the application of intelligence can buy:  .
.
This does not change the intelligence-maximizing allocation of intelligence between trading for hardware and self-improving.
Declining hardware costs
We might also expect the long-run trend in the cost of computing hardware to continue. This can again be modeled as an exponential process over time,  . The new expression for the growth of hardware is
. The new expression for the growth of hardware is  , identical in functional form to the expression representing wage growth, so again we can conclude that
, identical in functional form to the expression representing wage growth, so again we can conclude that  .
.
Maximizing profits rather than intelligence
AI projects might not reinvest all available resources in increasing the intelligence of the AI. They might want to return some of their revenue to investors if operated on a for-profit basis. (Or, if autonomous, they might invest in non-AI assets where the rate of return on those exceeded the rate of return on additional investments in intelligence.) On the other hand, they might borrow if additional money could be profitably invested in hardware for their AI.
If the profit-maximizing strategy involves less than 100% reinvestment, then whatever fraction of the AI's optimization power is reinvested should still follow the intelligence-maximizing allocation rule  , where
, where  is now the share of reinvested optimization power devoted to algorithmic improvements.
is now the share of reinvested optimization power devoted to algorithmic improvements.
If the profit-maximizing strategy involves a reinvestment rate of slightly greater than 100%, then at each moment the AI project will borrow some amount (net of interest expense on existing debts)  , so that the total optimization power available is
, so that the total optimization power available is  . Again, whatever fraction of the AI's optimization power is reinvested should still follow the intelligence-maximizing allocation rule
. Again, whatever fraction of the AI's optimization power is reinvested should still follow the intelligence-maximizing allocation rule  , where
, where  is now the share of economically augmented optimization power
is now the share of economically augmented optimization power  devoted to algorithmic improvements.
devoted to algorithmic improvements.
This strategy is no longer feasible, however, once  . Since by assumption hardware can be bought but algorithmic improvements cannot, at this point additional monetary investments will shift the balance of investment towards hardware, while 100% of the AI's own work is dedicated to self-improvement.
. Since by assumption hardware can be bought but algorithmic improvements cannot, at this point additional monetary investments will shift the balance of investment towards hardware, while 100% of the AI's own work is dedicated to self-improvement.